Interpreting IQR to identify outliers and data distribution

Introduction:

In statistics, the Interquartile Range (IQR) is a measure of the spread or dispersion of a dataset. It is a robust measure that is not affected by extreme values or outliers in the data. IQR is widely used in data analysis, especially in exploratory data analysis and outlier detection. In this article, we will discuss how to calculate IQR and interpret it to identify outliers and data distribution.It is calculated by using IQR calculator.

 

What is IQR?

The IQR is the range between the first quartile (Q1) and the third quartile (Q3) of a dataset. Quartiles are values that divide a dataset into four equal parts, where Q1 represents the 25th percentile and Q3 represents the 75th percentile. The IQR represents the range of values that lie within the middle 50% of the data, between Q1 and Q3.

 

How to calculate IQR?

To calculate the IQR of a dataset, follow these steps:

 

Step 1: Order the dataset from smallest to largest.

 

Step 2: Find the median of the dataset. This is the value that lies at the center of the dataset when it is ordered.

 

Step 3: Divide the dataset into two halves: the lower half and the upper half. If the median value is included in both halves, exclude it from both halves.

 

Step 4: Find the median of the lower half of the dataset. This is the first quartile (Q1).

 

Step 5: Find the median of the upper half of the dataset. This is the third quartile (Q3).

 

Step 6: Calculate the IQR by subtracting Q1 from Q3: IQR = Q3 - Q1.

 

Once you have calculated the IQR, you can use it to identify outliers and detect skewness in the data distribution.

 

Interpreting IQR

a. Identifying outliers using IQR:

One of the main applications of IQR is identifying outliers in a dataset. Outliers are values that are much larger or smaller than the other values in the dataset and can have a significant impact on statistical analyses. To identify outliers using IQR, we use the following rule:

 

An observation is considered an outlier if it falls below Q1 - 1.5 x IQR or above Q3 + 1.5 x IQR.

 

In other words, any value that is more than 1.5 times the IQR away from the lower or upper quartile is considered an outlier. This rule is known as the Tukey's boxplot rule.

 

b. Using IQR to detect skewness and data distribution:

Another application of IQR is to detect skewness and data distribution. Skewness is a measure of the asymmetry of a distribution, while data distribution describes the spread of values in a dataset. We can use IQR to detect skewness and data distribution by looking at the ratio of IQR to the overall range of the dataset.

 

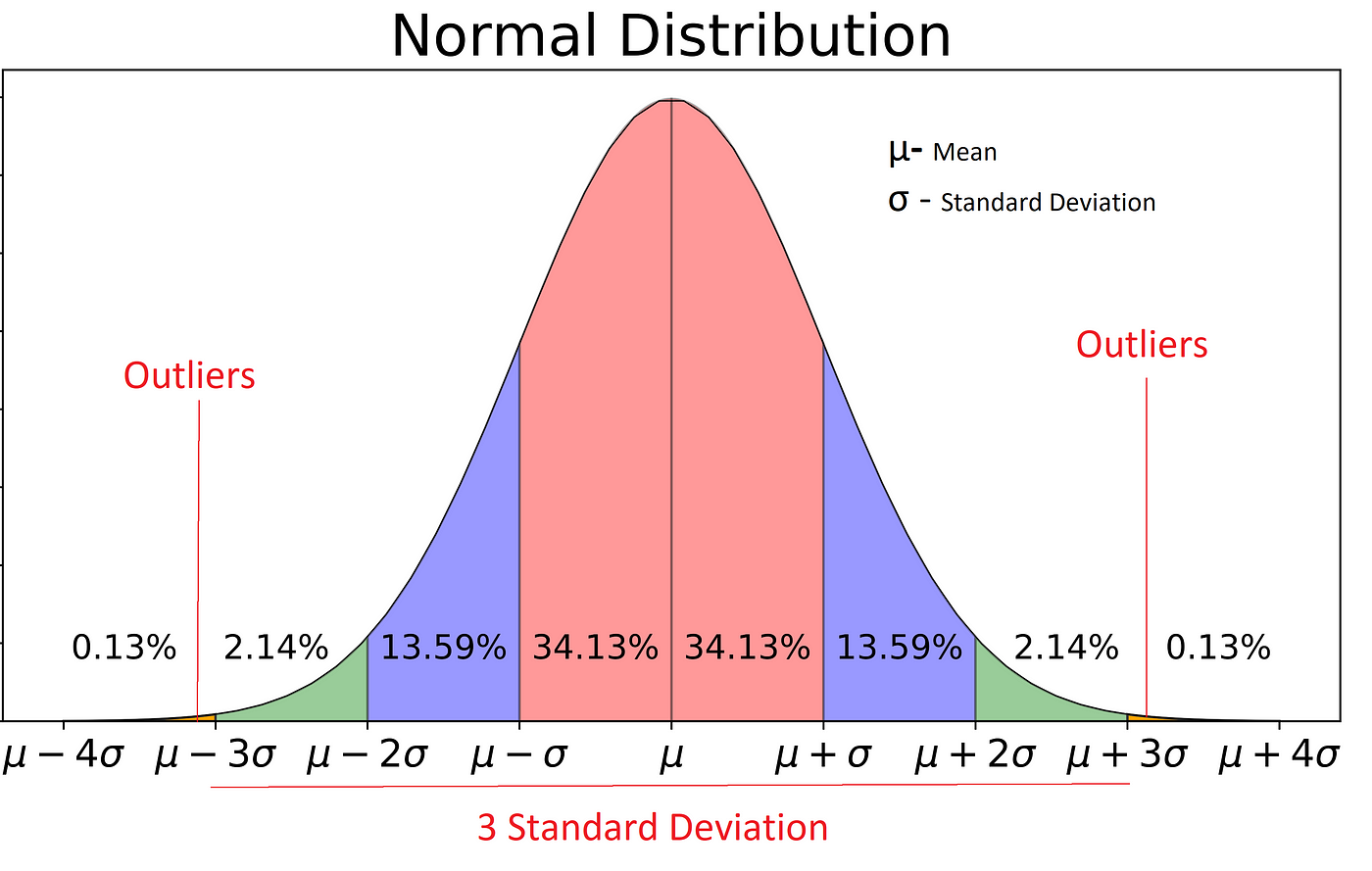
If the ratio of IQR to the range is small, it indicates that the data is spread out relatively evenly, and the distribution is likely to be symmetrical. On the other hand, if the ratio of IQR to the range is large, it indicates that the data is spread out unevenly, and the distribution is likely to be skewed.

 

For example, if the IQR of a dataset is 10 and the overall range is 50, the ratio of IQR to the range is 0.2. This indicates that the data is spread out relatively evenly, and the distribution is likely to be symmetrical. However, if the IQR of a dataset is 10 and the overall range is 20, the ratio of IQR to the range is 0.5. This indicates that the data is spread out unevenly, and the distribution is likely to be skewed.

 

By interpreting IQR, we can gain insights into the distribution and outliers of a dataset, which can help us make more accurate statistical inferences and predictions.

 

Examples

a: Example 1: 

Identifying outliers using IQR

Suppose we have the following dataset of test scores:

 

75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135

 

To identify outliers using IQR, we first need to calculate the quartiles and IQR. The median is 100, so the lower half of the dataset is:

 

75, 80, 85, 90, 95, 100

 

And the upper half of the dataset is:

 

105, 110, 115, 120, 125, 130, 135

 

The first quartile (Q1) is the median of the lower half of the dataset, which is 85. The third quartile (Q3) is the median of the upper half of the dataset, which is 120. Therefore, the IQR is:

 

IQR = Q3 - Q1 = 120 - 85 = 35

 

According to the Tukey's boxplot rule, any value that is more than 1.5 times the IQR away from Q1 or Q3 is considered an outlier. Using this rule, we can identify the outliers in the dataset:

 

Values below Q1 - 1.5 x IQR: 50 (outlier)

Values above Q3 + 1.5 x IQR: 150 (outlier)

Therefore, the outliers in this dataset are 50 and 150.

 

b. Example 2: 

Using IQR to detect skewness and data distribution

Suppose we have the following dataset of monthly salaries in a company:

 

$2,000, $2,200, $2,400, $2,600, $2,800, $3,000, $3,200, $3,400, $3,600, $3,800, $4,000, $4,200, $4,400, $4,600, $4,800

 

To use IQR to detect skewness and data distribution, we first need to calculate the quartiles and IQR. The median is $3,200, so the lower half of the dataset is:

 

$2,000, $2,200, $2,400, $2,600, $2,800, $3,000, $3,200

 

And the upper half of the dataset is:

 

$3,400, $3,600, $3,800, $4,000, $4,200, $4,400, $4,600, $4,800

 

The first quartile (Q1) is the median of the lower half of the dataset, which is $2,600. The third quartile (Q3) is the median of the upper half of the dataset, which is $4,200. Therefore, the IQR is:

 

IQR = Q3 - Q1 = $4,200 - $2,600 = $1,600

 

To calculate the range of the dataset, we subtract the smallest value from the largest value:

 

Range = $4,800 - $2,000 = $2,800

 

The ratio of IQR to the range is:

 

IQR/Range = $1,600/$2,800 = 0.57

 

Since the ratio of IQR to the range is greater than 0.3, we can conclude that the data is skewed and the distribution is not symmetrical. Specifically, the data is skewed to the right, as the upper half of the dataset has a larger range than the lower half.

 

Conclusion:

Interquartile range (IQR) is a useful statistical tool that provides information about the spread and distribution of a dataset. IQR is calculated as the difference between the third quartile (Q3) and the first quartile (Q1), and it is used to identify outliers and detect skewness and data distribution.

 

Identifying outliers using IQR involves calculating the quartiles, finding the IQR, and using the Tukey's boxplot rule to identify any values that are more than 1.5 times the IQR away from Q1 or Q3. Using IQR to detect skewness and data distribution involves calculating the quartiles, finding the IQR and range, and calculating the ratio of IQR to range. If the ratio is greater than 0.3, the data is considered skewed and the distribution is not symmetrical.

 

IQR is widely used in data analysis, and it is a valuable tool for identifying and understanding the properties of a dataset.

 

References:

 

Hyndman, R. J., & Fan, Y. (1996). Sample quantiles in statistical packages. The American Statistician, 50(4), 361-365.

Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.

 

Appendices

FAQ’s

 

Can outliers be present even if the IQR is small?

Yes, outliers can still be present even if the IQR is small. IQR is a measure of the spread of the middle 50% of the data, so it is possible for outliers to exist outside this range. Additionally, the Tukey's boxplot rule, which is often used to identify outliers based on the IQR, is not perfect and may not always capture all outliers in a dataset.

 

What should I do if I find outliers in my dataset using IQR?

If you identify outliers in your dataset using IQR, you may want to consider whether they are genuine data points or errors. If they are genuine data points, you may need to decide whether to remove them or keep them in your analysis. If they are errors, you should correct them if possible or remove them from your analysis.

 

How can I use IQR to determine the type of data distribution?

You can use IQR to determine the type of data distribution by comparing it to the range of the dataset. If the ratio of IQR to range is less than or equal to 0.3, the data is considered roughly symmetrical and normally distributed. If the ratio is greater than 0.3, the data is considered skewed and the distribution is not symmetrical. This can help you to determine which statistical methods are appropriate for analyzing the data.

Additional Resources 

https://iqrcalculator.com